| 概要(TOP) ラッパ型尺八 尺八と言えるか 春慶塗風尺八 長D管 プロフィール |
開口端効果の分離 |
|
開口端効果の分離
|
開口端効果の合計を計算する
開口端効果空気中の筒は、実際の筒長さよりも長い波長で共振してしまい下の模式図のように筒から飛び出した位置で振動します。
この図の筒から飛び出した部分を開口端効果と言います。開口端補正といわれる場合もありますが同じ意味です。
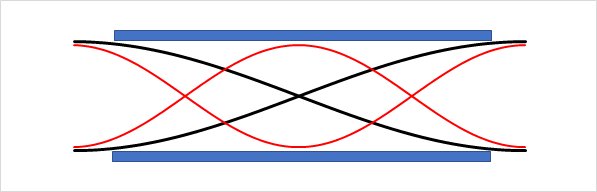
尺八は歌口と管尻または手孔を両端とする筒として空気が振動します。
筒音の場合は歌口と管尻、その他の音は歌口と手孔が両端になります。
全長L
全長Lと記していますのは上の図の振動部分の長さです。
実際の筒の長さと開口端効果を加えた長さになります。
全長
私がここで用いている全長というのは頭頂から管尻までの実際の長さの意味です。
Lを付けていません。
Lを付けた全長Lは開口端効果を含めた長さです。
開口端効果の分離計算
前項「4-4管尻の切断」で測定されていますが全長L=1181mm
全長=1063mm
です。
全長Lは歌口の開口端効果ΔUと、本体長さの全長1063と、管尻の開口端効果ΔSの合計です。
全長L=1181 =(ΔU+1063+ΔS)
ですが、ΔUとΔSがそれぞれいくらなのか分離しなくてはなりません。
ΔUの値がわかっていませんと、手孔の位置を求めることができないからです。
ΔSは単純な管の開口端効果ですから筒の内半径22mmの0.6倍と考えることができます。
このことはウイキペディアに詳しく示されています。
ΔS=0.6*22=13mmとなります。
上記の全長Lの計算式から
ΔU=1181-1063-ΔS = 1181-1063-13 = 105mm
となります。
管尻で実際の長さよりも13mm、歌口で実際の長さよりも105mm長くなって空気が振動するわけです。
歌口部分の開口端効果は思った以上に大きいことに驚かされます。
舌面の穴の削りを小さくしますと更に大きくなりますし、もっと大きな穴にすれば歌口の開口端効果は小さくなります。
歌口の適正な開口端効果の決定
今述べました開口端効果は私の場合の値です。
論文発表は見ていませんが、開口端効果は周波数に依存しないというのが定説のようですけれども、実際にはそうではないことを私は実験により確かめています。
開口端効果が比較的小さい場合は確かにあまり周波数に関係しませんが、この歌口のような値以上になってきますと周波数の影響を受けてきます。
甲の音や大甲の音を出してみますと、2倍音、4倍音とずれてくるのです。
このことから特に歌口の開口端効果ΔUはなるべく小さくしたいわけです。
小さくするには歌口の穴を大きくすればよろしいです。
ところが、孔を大きくするに従い、演奏時の息の量が大きく必要になってきます。音量も増して大変良いのですが、譜面の息継ぎから息継ぎまで持たなくなってしまいます。
肺活量が大きく息の続く方は孔を大きくしてΔUを小さくした方が良いと思います。
私の場合、この周波数依存性と、息の必要量のせめぎあいから孔の大きさを決定した結果、ΔUは105mmとなったわけです。
この値で周波数依存性は無視できる程度となり、十分甲の音は許容範囲に入ってくれます。
余談ですが、歌口の部品を作るとき、内面に面取りを施しましたが、この面取りをしませんとΔUはもっと大きくなってしまいます。
次項から手孔位置の計算を行います。