| 概要(TOP) ラッパ型尺八 尺八と言えるか 春慶塗風尺八 長D管 プロフィール |
基礎的事項 開口端効果 |
|
基礎的事項 開口端効果
|
注 このページは読み飛ばしていただいても結構です。
開口端効果とは
両端の開いた筒の共振周波数fは、筒の長さをL、音速をv、波長をλで表す場合、
λ/2=L
λ=2L
f=v/λ
=v/(2L)
となるように思われますが、実際にはそうではありません。
この図をご覧ください。
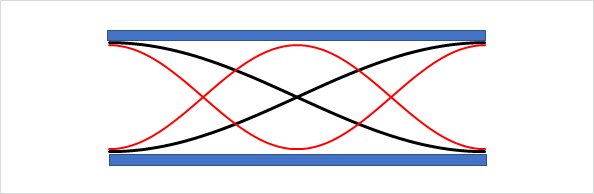
この2つの図は定在波として共振している時の空気分子の運動速度を模式的に表したものです。
上の図は上記のようにλ/2=Lとなっている状態を示しています。
下の図は実際の場合の状態を示しています。このように振動が筒から飛び出していることを開口端効果といいます。
開口端効果は開口端補正とも言われますが、同じ意味です。
λ/2=Lとなっている状態
λ/2=L+Δとなっている状態 (実際の状態)
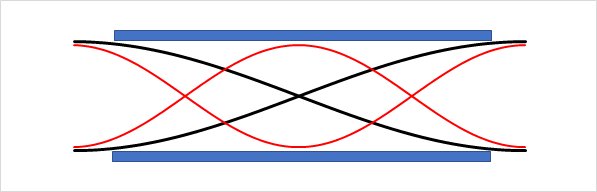
下の図は空気の振動が筒から飛び出しています。
その飛び出し分の合計をΔで示しています。
従いまして、実際の場合の共振周波数fは、
λ/2=L+Δ
λ=2(L+Δ)
f=v/λ
=v/2/(L+Δ)
となって、振動の長さは筒の長さよりΔだけ長くなったようになるわけです。
尺八における開口端効果
尺八は単純な筒ではありません。一方の開口部は歌口部分になり、他方の開口部は管尻又は手孔になります。
歌口部の開口端の面積は、舌面に切られたU字状の穴と、唇との間にできている空間の面積になります。
他方の開口端の面積は管尻の面積になる場合と、手孔の面積になる場合があります。
開口端効果は開口部の面積と筒の断面積の比率によって変わってきます。
一般に、開口部の面積が筒の断面積に対して小さくなるほど開口端効果は大きくなり、合計Δを増加させます。
唇を近づけて歌口部の開口端面積を小さくしますと、Δが増加し、fは小さくなります。
音が下がるわけです。
これはメリの状態を示しています。
反対に唇を遠ざければΔが小さくなってfが大きくなりますから、カリの状態を示すことになります。
開口端効果について詳しくはウイキペディアに乗っています。
単純な管の場合、開口端補正は管半径の0.6倍から0.8倍と記されています。
このことは、管尻の開口端効果を計算するのに役立ちます。
また、開口端の面積が管の断面積より小さくなるとどのように変化するかは静岡県立科学技術高等学校の研究結果として発表されています。
この中に、「図 10 を見ると、面積率が大きくなるほど開口端補正が小さくなる傾向が見られた。」と記されています。
ここでの面積率とは、「開口端面積/管断面積」を言われているようです。
この研究は、歌口や手孔の開口端効果を計算するのに役立ちます。
開口端効果についての注意事項
開口端効果は色々の条件によってわずかですが変わってきます。1 温度によって開口端効果の値は変わってきます。
2 開口端面積が筒断面積に等しい場合は、開口端効果は周波数に影響されないといわれていますが、そうでない場合は影響を受けるようです。
3 筒から開口端に至るのでの間に段差や絞り、細い部分など不連続部がある場合、その影響を開口端効果に含めて考えると便利ですが、その値は周波数の影響を受けやすくなります。
上記1は音速が変わりますから当然のことです。開口端効果を考える場合には温度を決めないといけません。
2と3は手孔のある場所の肉厚に関係していますし歌口の構造にも関係します。
どのように構造を変えるとどのように開口端効果が変わってくるかはわかっていません。実際に試してみるより仕方ないようです
基本方程式
尺八の設計にあたって基本的な方程式を立てることができます。ΔU 歌口の開口端効果
ΔA 手孔の開口端効果
ΔS 管尻の開口端効果
L 頭部から手孔中心または管尻に至る距離
R 筒の内半径
f 周波数
v 音速
ある周波数fを筒音として発生する場合の方程式
λ=v/f
λ/2=L+ΔU+ΔS
ΔS=0.6×R
温度tに対する音速vはウイキペディアに示されていますが、v=331.5 + 0.61 t (m/s)です。
手孔をあける前に音を出して調律計などで周波数fを測定してみますと、
λがわかり、ΔSもわかりますので、歌口部のΔUを算出することができます。
ここで管尻までの長さを調整したり歌口の削りを調整したりして筒音を希望の周波数fにしておきます。
ここで求められたΔUを使って手孔位置を求めることができます。
希望する手孔の周波数fを決めます。
手孔の場合の方程式は
λ=v/f
λ/2=L+ΔU+ΔA
であり、ΔAは静岡県立科学技術高等学校の研究結果の図10から算定できます。
したがって、
L=λ/2-ΔU-ΔA
として求めることができます。